Practical applications of artificial neural networks (ANNs) for control systems, especially for non-linear systems, include simulating time-optimal controllers and for ANN-based controlled system (plant) models. Such models, combined with classical proportional-integral-derivative (PID) controllers, can enable adaptive and other, more sophisticated, control systems.
Learning Objectives
- Examine the basics of neural networks.
- Look at a neural network implementation in Python.
- Learn how neural networks are suitable for control applications, with examples of control systems with ANN.
When reading the title, “Introduction to artificial neural networks in control applications,” you might ask if it’s worth reading more about artificial neural networks (ANN), successfully resolved decades ago, especially with thousands of ANN articles on the internet. (Answer is: “Yes.” Please continue.)
When I became interested in ANN, I went through hundreds of ANN articles. Only a handful helped me to understand how the ANN work and can be implemented. Even so, I couldn’t find any article about how a control system using an ANN could be implemented. I spent hundreds of hours experimenting with Python programming and ANN and control systems simulations, until I became satisfied with my understanding of how an ANN works in control system applications.
Today’s professionals don’t have to solve ANN problems from the scratch. They can use elaborated libraries of classes, functions, etc., provided in the support materials (libraries) of many programing platforms/languages. However, if you need to first understand ANN basics for control systems, then this article should help.
Download the .pdf to learn more.
1. Basics of neural networks
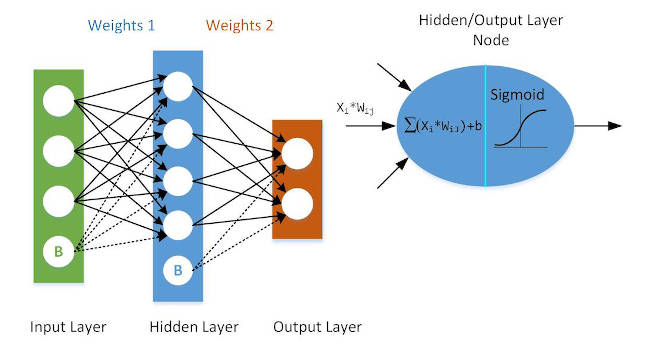
Neural networks are trying to imitate abilities of the human and animal brains. The most important of those abilities is adaptability. While modern computers can outperform human brain in many ways, they are still “static” devices, and that’s why computers can’t use all their potential. The use of artificial neural networks tries to introduce brain functionalities to a computer by copying behavior of nervous systems. We can imagine a neural network as a mathematical function that maps a given input set to a desired output set. Neural networks consist of the following components:
- one input layer, x,
- one or more hidden layers,
- one output layer, ŷ,
- a set of weights and biases between each layer, W and b,
- activation function for each hidden layer, σ.
Figure 1 shows the architecture of a 2-layer neural network. (Note: The input layer is typically excluded when counting the number of layers in a neural network.) Biases are shown as an additional neuron (node) in the input and in the hidden layer, having a fixed, non-zero value, for example 1, which is modified (multiplied) with the specific weight coefficient values before they are added to the next layer nodes sums.
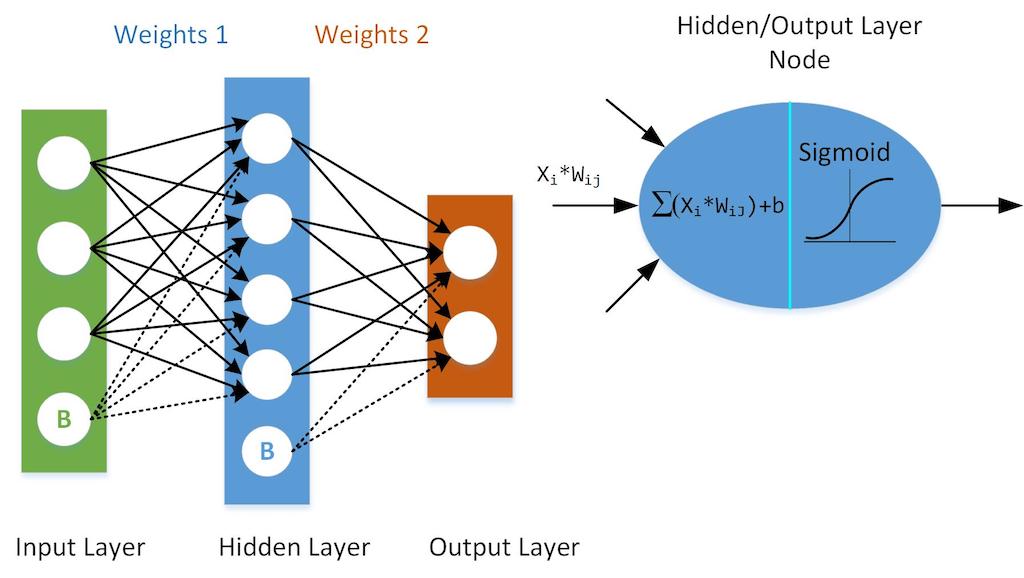
On the right-hand side of Figure 1, see one such (j-th) node of a hidden layer. At first, it sums up all the signals coming from the input (i-th) nodes, each affected – multiplied by its weight coefficient. Before the sum leaves the node output, it goes through an activation function – limiter. The most popular limiter is implemented by the Sigmoid function, S(x), as it can be relatively simply differentiated:
S(x) = 1 / (1 + e-x)
Similar nodes are used in the output layer. Just their input signals are coming from the nodes of the hidden layer.
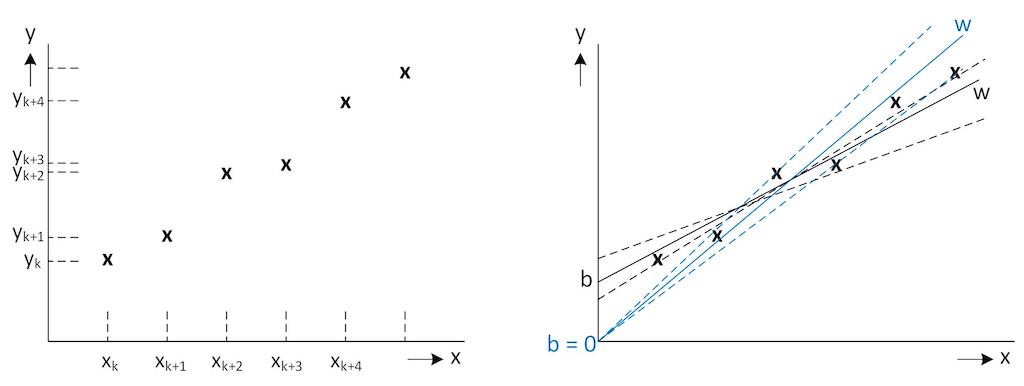
The right values of the weight coefficients determine the strength of the predictions, that is, the precision with which the input set will be transformed into the output set. Figure 2 shows a typical input → output set mapping (on the left side) and how the ANN can approximate such mapping by a linear function y = W x + b (on the right side). A suitable mapping can be found even without applying bias (offset), but generally adding the offset (bias) should yield better approximation. Adding more hidden layers allows even a non-linear mapping.
A process of fine-tuning of the weight coefficients from the input and hidden layers nodes is known as training the neural network. Each iteration of the training process consists of the following steps:
- Calculation of the predicted output ŷ, a process known as feedforward
- Updating the weight coefficients, a process known as backpropagation
The output ŷ of a simple 2-layer neural network is calculated as:
ŷ = ϐ(W2ϐ(W1x + b1) + b2)
The predicted output, , will naturally differ from the desired output, , at least at the beginning of the training process. How much it differs will tell us the Loss Function. There are many available loss functions, but a simple, sum-of-squares error is a good loss function.
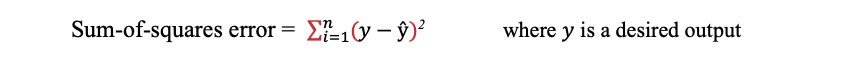
Our goal in training is to find the best set of weights that minimizes the loss function. Mathematically speaking, we need to find a loss function extreme (a minimum in our case). Such a loss function doesn’t depend on just one variable (x). It can be a multidimensional function having a complex shape with many local minimums. Our goal is to find a global minimum of the loss function.
Let’s find a first derivation of the sum-of-squares error function, ∂Loss(y,ŷ)/∂W. Unfortunately, our loss function does not depend directly on the weight coefficients, so we need to apply the following chain rule for its derivation calculation:
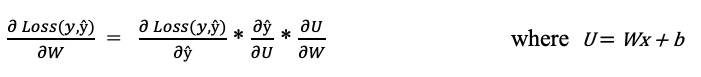
The first partial derivation yields: 2(y – ŷ )
the second partial derivation yields: ϐ’
and the last partial derivation is just: x
At the end we will get: ∂Loss(y,ŷ)/∂W = 2(y – ŷ) * ϐ’ * x and this is what we will have to implement as the backpropagation process. An advantage of using the Sigmoid function is a simple implementation of its derivative, ϐ’ :
ϐ’(u) = ϐ(u)(1 – ϐ(u))
The formula above describes how to proceed: Back propagate from the output of the neural network to the hidden layer, which lays in front of the output layer, and which is connected with the output layer via the W2 weights. The same process has to be applied again going from the hidden layer to the input layer, which is connected with the hidden layer via the W1 weights. The first chain member in the loss function derivation at the hidden layer, ∂Loss(h,ĥ)/∂ĥ, will have to be calculated differently, as we don’t explicitly know desired values of the hidden layer, h. We will have to calculate them from the output values, as you will see in the following paragraph.
If reading in the digital edition, click the headline to get to the online article, to download a 17-page PDF, with a Python (a suitable programming platform for the neural networks) programming tutorial, with more equations and diagrams to explain and links to related resources.
2. Neural networks implementation in Python
3. Neural networks suitable for control applications
4. Examples of control systems with ANN
4.1 ANN simulation of feed-forward and feedback controller
5. Conclusion: ANN use for control systems
Peter Galan is a retired control software engineer; Edited by Mark T. Hoske, content manager, Control Engineering, www.controleng.com, CFE Media and Technology, www.cfemedia.com, [email protected].
KEYWORDS
Artificial neural networks (ANN), ANN for control systems
LEARNING OBJECTIVES
CONSIDER THIS
Could an artificial neural network (ANN) enhance your control system or plant models?
ONLINE extra
Other Control Engineering articles by Peter Galan, retired control software engineer are highlighted below.