We explore one of the trickiest problem to overcome with a feedback controller – process dead time. The Smith predictor could be the solution.
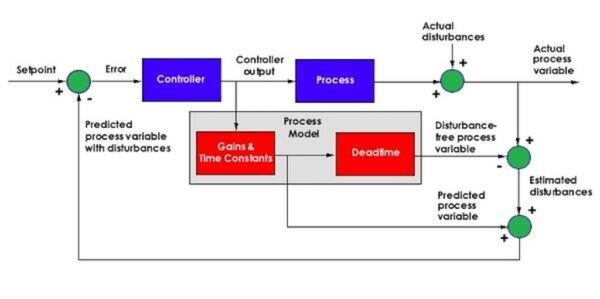
Arguably the trickiest problem to overcome with a feedback controller is process dead time – the delay between the application of a control effort and its first effect on the process variable. During that interval, the process does not respond to the controller’s activity at all, and any attempt to manipulate the process variable before the dead time has elapsed inevitably fails.
Dead time in control applications
Dead time occurs in many different control applications, generally as a result of material being transported from the site of the actuator to another location where the sensor takes its reading. Not until the material has reached the sensor can any changes caused by the actuator be detected. Consider, for example, the rolling mill, which produces a continuous sheet of some material at a rate of inches per second. A feedback controller uses a piston to modify the gap between a pair of reducing rollers that squeezes the material into the desired thickness. The dead time in this process is caused by the separation between the rollers and the thickness gauge.

The controller in this example can compare the current thickness of the sheet (the process variable) with the desired thickness (the set-point) and generate an output, but it must wait at least D S/V seconds for the thickness of the sheet to change. If it expects a result any sooner, it will determine that its last control effort had no effect and will continue to apply ever larger corrections to the rollers until the sensor begins to see the thickness changing in the desired direction. By that time, however, it will be too late. The controller will have already overcompensated for the original thickness error, perhaps to the point of causing an even larger error in the opposite direction.
How badly the controller overcompensates depends on how aggressively it is tuned and on the difference between the actual and the assumed dead time. That is, if the controller assumes the dead time is much shorter than is actually the case, it will spend a much longer time increasing its output before successfully effecting a change in the process variable. If the controller is tuned to be particularly aggressive, the rate at which it increases its output during that interval will be especially high.
How to overcome dead time in control applications
Curing overcompensation means addressing one or both symptoms. The easiest solution is to detune the controller to slow response rate. A detuned controller won’t have time to overcompensate unless dead time is very long.
The integrator in a PID controller is particularly sensitive to dead time. By design, its function is to continue ramping up the controller’s output so long as there is an error between the set-point and the process variable. In the presence of dead-time, the integrator works overtime. Ziegler and Nichols determined the best way to detune a PID controller to handle a dead time of D seconds is reduce the integral tuning constant by a factor of D2. Also, the proportional tuning constant should be reduced by a factor of D. The derivative term is unaffected by dead time. It only occurs after the process variable begins to move.
Detuning can restore stability to a control loop that suffers from chronic overcompensation, but it would not even be necessary if the controller could first be made aware of the dead time, then endowed with the patience to wait it out. That is essentially what happens in the famous Smith predictor control strategy proposed in 1957 by O.J.M. Smith, a professor at the University of California at Berkeley.
The Smith predictor
Smith’s strategy consists of an ordinary feedback loop plus an inner loop that introduces two extra terms directly into the feedback path. The first term is an estimate of what the process variable would look like in the absence of any disturbances. It is generated by running the controller output through a process model that intentionally ignores the effects of load disturbances. If the model is otherwise accurate in representing the behavior of the process, its output will be a disturbance-free version of the actual process variable.
The mathematical model used to generate the disturbance-free process variable has two elements connected in series. The first represents all of the process behavior not attributable to dead time. The second represents nothing but the dead time. The dead time-free element is generally implemented as an ordinary differential or difference equation that includes estimates of all the process gains and time constants. The second element is simply a time delay. The signal that goes into it comes out delayed but otherwise unchanged.
The second term Smith’s strategy introduces into the feedback path is an estimate of what the process variable would look like in the absence of both disturbances and dead time. It is generated by running the controller output through the first element of the process model (the gains and time constants) but not through the time delay element. It predicts what the disturbance-free process variable will be once the dead time has elapsed, hence the expression Smith predictor.
A feedback variable that excludes dead time
Subtracting the disturbance-free process variable from the actual process variable yields an estimate of the disturbances. By adding this difference to the predicted process variable, Smith created a feedback variable that includes the disturbances but not the dead time.
So what? The Smith predictor can show an estimate of the process variable (with both disturbances and dead time) generated by adding the estimated disturbances back into the disturbance-free process variable. The result is a feedback control system with the dead time outside of the loop.
The Smith predictor works to control the modified feedback variable (the predicted process variable with disturbances included) rather than the actual process variable. If it is successful in doing so, and if the process model does indeed match the process, then the controller will simultaneously drive the actual process variable towards the set-point whether the set-point changes or a load disturbs the process.
Not as easy as it looks
Unfortunately, those are big ifs. It’s easier for the controller to meet its objectives without dealing with the dead time, but it is not always a simple matter to generate the process models needed to make the strategy work. Even the slightest mismatch between the process and the model can cause the controller to generate an output that successfully manipulates the modified feedback variable but drives the actual process variable off into oblivion. There have been several fixes proposed to improve on the basic Smith predictor, but dead time remains a particularly difficult control problem.
This article originally appeared May 1, 1996.